HOME»ネットワークスペシャリスト平成21年秋期»午前Ⅰ 問3
ネットワークスペシャリスト平成21年秋期 午前Ⅰ 問3
問3
n個の要素x1,x2,…,xnから成る連結リストに対して,新たな要素xn+1の末尾への追加に要する時間をƒ(n)とし,末尾の要素xnの削除に要する時間をg(n)とする。nが非常に大きいとき,実装方法1と実装方法2におけるg(n)ƒ(n)の挙動として,適切なものはどれか。
〔実装方法1〕
先頭のセルを指すポインタ型の変数 front だけをもつ。 〔実装方法2〕
〔実装方法2〕
先頭のセルを指すポインタ型の変数 front と,末尾のセルを指すポインタ型の変数 rear を併せもつ。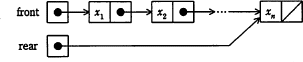
〔実装方法1〕
先頭のセルを指すポインタ型の変数 front だけをもつ。

先頭のセルを指すポインタ型の変数 front と,末尾のセルを指すポインタ型の変数 rear を併せもつ。

分類 :
テクノロジ系 » アルゴリズムとプログラミング » データ構造
正解 :
イ
解説 :
2つの連結構造(単方向リスト・双方向リスト)において、
※一回のポインタ参照→次のセルへのアクセスに要する時間は一定であるとし、処理に要する時間は、このセル移動に回数に比例するものとします。
まず〔実装方法1〕について考えます。
"新要素(n+1)の末尾への追加"は、 ポインタfrontからリスト構造を末尾のデータ(n)まで順にたどり、末尾のデータのポインタ部を新しい要素へのポインタにします。したがって、セル移動の回数はn回です。
"末尾の要素の削除"は、ポインタ front から末尾の要素の一つ前の手前の要素(n-1)までたどり、末尾の要素へのポインタを削除します。したがって、セル移動の回数はn-1回です。
nは非常に大きいという条件があるので、〔実装方法1〕のg(n)ƒ(n)は、n-1nでほぼ1となります。
次に〔実装方法2〕について考えます。
"新要素(n+1)の末尾への追加"は、 ポインタ rear を参照することで1回で末尾のセルへアクセスし、末尾のデータのポインタ部を新しい要素へのポインタにします。したがって、セル移動の回数は1回です。
"末尾の要素の削除"は〔実装方法1〕と同様に、ポインタ front から末尾の要素の一つ前の手前の要素(n-1)までたどり、末尾の要素へのポインタを削除します。この場合では、ポインタ rear から末尾のセルへ移動することはできても、末尾のセルからその一つ手前のセルへはポインタがないため戻ることができないという点が理解できているかがポイントになります。したがって、セル移動の回数はn-1回です。
〔実装方法2〕のg(n)ƒ(n)は、n-11でほぼnに比例となります。
以上より、〔実装方法1〕が"ほぼ1となる"、〔実装方法2〕が"ほぼnに比例する"の組合せで「イ」が正解となります。
- 新要素の末尾への追加 ƒ(n)
- 末尾の要素の削除 g(n)
※一回のポインタ参照→次のセルへのアクセスに要する時間は一定であるとし、処理に要する時間は、このセル移動に回数に比例するものとします。
まず〔実装方法1〕について考えます。
"新要素(n+1)の末尾への追加"は、 ポインタfrontからリスト構造を末尾のデータ(n)まで順にたどり、末尾のデータのポインタ部を新しい要素へのポインタにします。したがって、セル移動の回数はn回です。
"末尾の要素の削除"は、ポインタ front から末尾の要素の一つ前の手前の要素(n-1)までたどり、末尾の要素へのポインタを削除します。したがって、セル移動の回数はn-1回です。
nは非常に大きいという条件があるので、〔実装方法1〕のg(n)ƒ(n)は、n-1nでほぼ1となります。
次に〔実装方法2〕について考えます。
"新要素(n+1)の末尾への追加"は、 ポインタ rear を参照することで1回で末尾のセルへアクセスし、末尾のデータのポインタ部を新しい要素へのポインタにします。したがって、セル移動の回数は1回です。
"末尾の要素の削除"は〔実装方法1〕と同様に、ポインタ front から末尾の要素の一つ前の手前の要素(n-1)までたどり、末尾の要素へのポインタを削除します。この場合では、ポインタ rear から末尾のセルへ移動することはできても、末尾のセルからその一つ手前のセルへはポインタがないため戻ることができないという点が理解できているかがポイントになります。したがって、セル移動の回数はn-1回です。
〔実装方法2〕のg(n)ƒ(n)は、n-11でほぼnに比例となります。
以上より、〔実装方法1〕が"ほぼ1となる"、〔実装方法2〕が"ほぼnに比例する"の組合せで「イ」が正解となります。
出典
- 応用情報技術者平成21年秋期 問5と同題

