HOME»ネットワークスペシャリスト令和5年春期»午前Ⅰ 問7
ネットワークスペシャリスト令和5年春期 午前Ⅰ 問7
問7
NAND素子を用いた次の組合せ回路の出力Zを表す式はどれか。ここで,"・"は論理積,"+"は論理和,"X"はXの否定を表す。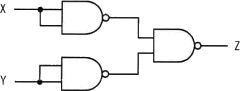

- X・Y
- X+Y
- X・Y
- X+Y
分類 :
テクノロジ系 » ハードウェア » ハードウェア
正解 :
イ
解説 :
NAND回路は、NAND(Not AND)の名称どおりAND回路の逆を出力する回路で、2つの入力がともに"1"のときだけ"0"を出力し、それ以外の入力では"1"を出力します。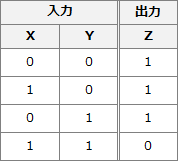 設問の回路に入力値XとYのすべての組合せ(X=0,Y=0・X=1,Y=0・X=0,Y=1・X=1, Y=1)を試すと、それぞれ以下の出力が得られます。
設問の回路に入力値XとYのすべての組合せ(X=0,Y=0・X=1,Y=0・X=0,Y=1・X=1, Y=1)を試すと、それぞれ以下の出力が得られます。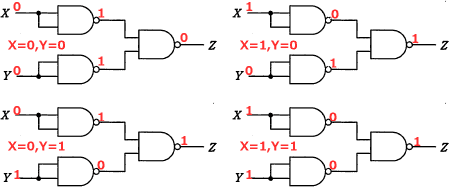 上記結果の入力値XとYおよび出力値Zの関係を整理すると、次の真理値表が得られます。
上記結果の入力値XとYおよび出力値Zの関係を整理すると、次の真理値表が得られます。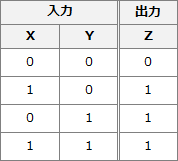 この真理値表より、設問の回路は2つの入力の論理和を得るOR回路と等価であることがわかるので、正解は「X+Y」です。
この真理値表より、設問の回路は2つの入力の論理和を得るOR回路と等価であることがわかるので、正解は「X+Y」です。
【別解】
回路図を論理式で表し、その論理式を変形することで答えを導く解く方法もあります。
Z=X・X・Y・Y
=X・X+Y・Y //ド・モルガンの法則を適用
=X・X+Y・Y //A=A
=X+Y //A・A=A



【別解】
回路図を論理式で表し、その論理式を変形することで答えを導く解く方法もあります。
Z=X・X・Y・Y
=X・X+Y・Y //ド・モルガンの法則を適用
=X・X+Y・Y //A=A
=X+Y //A・A=A
出典
- 応用情報技術者令和5年春期 問21と同題
